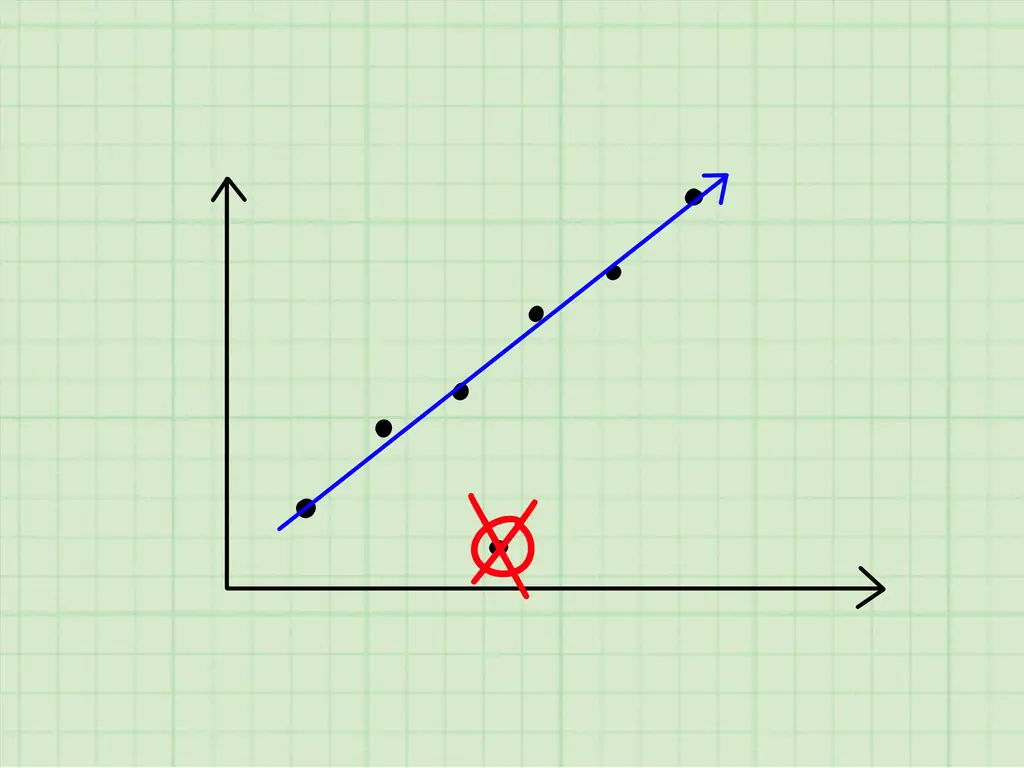
В Правило 72 это удобный инструмент, используемый в финансах для оценки количества лет, которое потребуется, чтобы удвоить денежную сумму за счет выплаты процентов при определенной процентной ставке. Правило также позволяет оценить годовую процентную ставку, необходимую для удвоения денежной суммы за определенное количество лет. Правило гласит, что процентная ставка, умноженная на период времени, необходимый для удвоения суммы денег, приблизительно равна 72.
Правило 72 применимо в случаях экспоненциального роста (как в случае сложных процентов) или экспоненциального «спада», как в случае потери покупательной способности, вызванной денежной инфляцией.
Шаги
Метод 1 из 4. Оценка времени «удвоения»

Шаг 1. Пусть R x T = 72
R - это скорость роста (годовая процентная ставка), а T - время (в годах), необходимое для того, чтобы сумма денег удвоилась.

Шаг 2. Вставьте значение для R
Например, сколько времени нужно, чтобы превратить 100 долларов в 200 долларов при годовой процентной ставке 5%? Полагая R = 5, получаем 5 x T = 72.

Шаг 3. Найдите неизвестную переменную
В этом примере разделите обе части приведенного выше уравнения на R (то есть 5), чтобы получить T = 72 ÷ 5 = 14,4. Таким образом, удвоение 100 долларов при процентной ставке 5% годовых занимает 14,4 года. (Начальная сумма не имеет значения. Чтобы удвоиться, потребуется одинаковое количество времени, независимо от начальной суммы.)

Шаг 4. Изучите эти дополнительные примеры:
- Сколько времени нужно, чтобы удвоить сумму денег по ставке 10% годовых? 10 x T = 72. Разделите обе части уравнения на 10, так что T = 7,2 года.
- Сколько времени нужно, чтобы превратить 100 долларов в 1600 долларов по ставке 7,2% годовых? Помните, что 100 должны удвоиться четыре раза, чтобы достичь 1600 (100 → 200 долларов, 200 → 400 долларов, 400 → 800 долларов, 800 → 1600 долларов). Для каждого удвоения 7,2 x T = 72, поэтому T = 10. Итак, поскольку каждое удвоение занимает десять лет, общее время, необходимое (для преобразования 100 долларов в 1600 долларов), составляет 40 лет.
Метод 2 из 4: оценка скорости роста

Шаг 1. Пусть R x T = 72
R - скорость роста (процентная ставка), а T - время (в годах), которое требуется, чтобы удвоить любую сумму денег.

Шаг 2. Введите значение T
Например, предположим, что вы хотите удвоить свои деньги за десять лет. Какая процентная ставка вам понадобится для этого? Введите 10 для T в уравнение. R х 10 = 72.

Шаг 3. Решите относительно R
Разделите обе части на 10, чтобы получить R = 72 ÷ 10 = 7,2. Таким образом, вам понадобится годовая процентная ставка в размере 7,2%, чтобы удвоить ваши деньги за десять лет.
Метод 3 из 4: Оценка экспоненциального «спада» (убытка)

Шаг 1. Оцените время, которое потребуется, чтобы потерять половину своих денег (или ее покупательную способность из-за инфляции). Пусть T = 72 ÷ R
Это то же уравнение, что и выше, только с небольшими изменениями. Теперь введите значение R. Пример:
-
Сколько времени потребуется 100 долларам, чтобы принять покупательную способность в 50 долларов при уровне инфляции 5% в год?
Пусть 5 x T = 72, так что T = 72 ÷ 5 = 14,4. Вот сколько лет потребуется, чтобы деньги потеряли половину своей покупательной способности в период инфляции в 5%. (Если уровень инфляции будет меняться из года в год, вам придется использовать средний уровень инфляции, который существовал за полный период времени.)

Шаг 2. Оцените скорость распада (R) за заданный промежуток времени:
R = 72 ÷ T. Введите значение T и решите относительно R. Например:
-
Если покупательная способность 100 долларов через десять лет станет 50 долларами, каков будет уровень инфляции за это время?
R x 10 = 72, где T = 10. Тогда R = 72 ÷ 10 = 7,2%
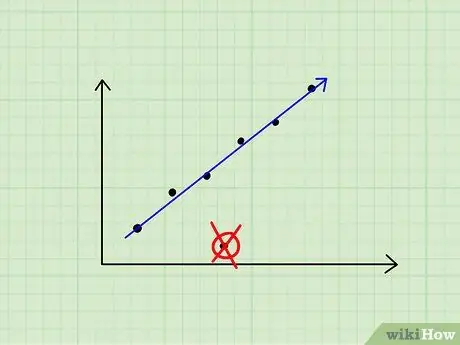
Шаг 3. Игнорируйте любые необычные данные
Если вы можете определить общую тенденцию, не беспокойтесь о временных числах, которые сильно выходят за пределы допустимого диапазона. Отбросьте их от рассмотрения.
График удвоения времени
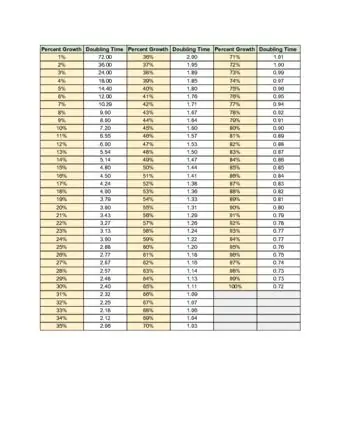
Пример временной диаграммы удвоения
Метод 4 из 4: вывод
Шаг 1. Понять, как работает деривация для периодического начисления сложных процентов
- Для периодического начисления сложных процентов FV = PV (1 + r) ^ T, где FV = будущая стоимость, PV = текущая стоимость, r = скорость роста, T = время.
- Если деньги удвоились, FV = 2 * PV, поэтому 2PV = PV (1 + r) ^ T или 2 = (1 + r) ^ T, если текущая стоимость не равна нулю.
- Решите относительно T, взяв натуральные бревна с обеих сторон и переставив, чтобы получить T = ln (2) / ln (1 + r).
- Ряд Тейлора для ln (1 + r) около 0 равен r - r2/ 2 + г3/ 3 -… Для малых значений r вклад членов с более высокой степенью мал, и выражение приближает r, так что t = ln (2) / r.
- Обратите внимание, что ln (2) ~ 0,693, так что T ~ 0,693 / r (или T = 69,3 / R, выражая процентную ставку R от 0 до 100%), что является правилом 69,3. Другие числа, такие как 69, 70 и 72, используются для упрощения вычислений.
Шаг 2. Понять, как работает деривация для непрерывного начисления процентов
Для периодического начисления сложных процентов с многократным начислением начислений в год будущая стоимость определяется как FV = PV (1 + r / n) ^ nT, где FV = будущая стоимость, PV = текущая стоимость, r = темп роста, T = время и n = количество периодов начисления сложных процентов в год. Для непрерывного сложения n стремится к бесконечности. Используя определение e = lim (1 + 1 / n) ^ n, когда n приближается к бесконечности, выражение становится FV = PV e ^ (rT).
- Если деньги удвоились, FV = 2 * PV, поэтому 2PV = PV e ^ (rT) или 2 = e ^ (rT), если текущая стоимость не равна нулю.
- Решите для T, взяв натуральные бревна с обеих сторон и переставив, чтобы получить T = ln (2) / r = 69,3 / R (где R = 100r, чтобы выразить скорость роста в процентах). Это правило 69.3.
-
Для непрерывного сложения 69,3 (или примерно 69) дает более точные результаты, поскольку ln (2) составляет примерно 69,3%, а R * T = ln (2), где R = скорость роста (или распада), T = удвоение (или уменьшение вдвое), а ln (2) - это натуральный логарифм 2, 70 также можно использовать в качестве приближения для непрерывного или ежедневного (что близко к непрерывному) сложения для простоты вычислений. Эти варианты известны как правило 69,3, Правило 69, или правило 70.
Аналогичная регулировка точности для правило 69,3 используется для высоких ставок с ежедневным начислением сложных процентов: T = (69,3 + R / 3) / R.
-
В Правило второго порядка Эккарта-Макхейла, или правило E-M, дает мультипликативную поправку к правилу 69,3 или 70 (но не 72) для большей точности для более высоких диапазонов процентных ставок. Чтобы вычислить приближение E-M, умножьте результат правила 69,3 (или 70) на 200 / (200-R), то есть T = (69,3 / R) * (200 / (200-R)). Например, если процентная ставка составляет 18%, Правило 69,3 говорит, что t = 3,85 года. Правило E-M умножает это на 200 / (200-18), давая время удвоения 4,23 года, что лучше соответствует фактическому времени удвоения 4,19 года при этой скорости.
Аппроксимация Паде третьего порядка дает еще лучшее приближение, используя поправочный коэффициент (600 + 4R) / (600 + R), то есть T = (69,3 / R) * ((600 + 4R) / (600 + R)). Если процентная ставка составляет 18%, аппроксимация Паде третьего порядка дает T = 4,19 года
- Чтобы оценить время удвоения для более высоких ставок, скорректируйте 72, добавляя 1 на каждые 3 процента, превышающие 8%. То есть T = [72 + (R - 8%) / 3] / R. Например, если процентная ставка составляет 32%, время, необходимое для удвоения данной суммы денег, равно T = [72 + (32 - 8) / 3] / 32 = 2,5 года. Обратите внимание, что здесь используется 80 вместо 72, что дает 2,25 года для времени удвоения.
- Вот таблица, в которой указано количество лет, необходимое для удвоения любой заданной суммы денег при различных процентных ставках, и сравнение приближения с различными правилами:
| Темп | Действительный | Правило | Правило | Правило | ЭМ |
|---|---|---|---|---|---|
| 0.25% | 277.605 | 288.000 | 280.000 | 277.200 | 277.547 |
| 0.5% | 138.976 | 144.000 | 140.000 | 138.600 | 138.947 |
| 1% | 69.661 | 72.000 | 70.000 | 69.300 | 69.648 |
| 2% | 35.003 | 36.000 | 35.000 | 34.650 | 35.000 |
| 3% | 23.450 | 24.000 | 23.333 | 23.100 | 23.452 |
| 4% | 17.673 | 18.000 | 17.500 | 17.325 | 17.679 |
| 5% | 14.207 | 14.400 | 14.000 | 13.860 | 14.215 |
| 6% | 11.896 | 12.000 | 11.667 | 11.550 | 11.907 |
| 7% | 10.245 | 10.286 | 10.000 | 9.900 | 10.259 |
| 8% | 9.006 | 9.000 | 8.750 | 8.663 | 9.023 |
| 9% | 8.043 | 8.000 | 7.778 | 7.700 | 8.062 |
| 10% | 7.273 | 7.200 | 7.000 | 6.930 | 7.295 |
| 11% | 6.642 | 6.545 | 6.364 | 6.300 | 6.667 |
| 12% | 6.116 | 6.000 | 5.833 | 5.775 | 6.144 |
| 15% | 4.959 | 4.800 | 4.667 | 4.620 | 4.995 |
| 18% | 4.188 | 4.000 | 3.889 | 3.850 | 4.231 |
| 20% | 3.802 | 3.600 | 3.500 | 3.465 | 3.850 |
| 25% | 3.106 | 2.880 | 2.800 | 2.772 | 3.168 |
| 30% | 2.642 | 2.400 | 2.333 | 2.310 | 2.718 |
| 40% | 2.060 | 1.800 | 1.750 | 1.733 | 2.166 |
| 50% | 1.710 | 1.440 | 1.400 | 1.386 | 1.848 |
| 60% | 1.475 | 1.200 | 1.167 | 1.155 | 1.650 |
| 70% | 1.306 | 1.029 | 1.000 | 0.990 | 1.523 |
Видео - с помощью этой службы некоторая информация может быть передана YouTube
подсказки
-
Пусть Правило 72 работает на вас. начинаю экономить сейчас.
При темпах роста 8% в год (приблизительная норма прибыли на фондовом рынке) вы удвоите свои деньги за девять лет (72 ÷ 8 = 9), увеличите свои деньги в четыре раза за 18 лет и получите в 16 раз больше денег. в 36 лет.
- Вы можете использовать следствие Феликса из правила 72 для расчета «будущей стоимости» аннуитета (то есть, какой будет номинальная стоимость аннуитета в указанное время в будущем). Вы можете прочитать о выводе на различных финансовых и инвестиционных сайтах.
- Значение 72 было выбрано в качестве удобного числителя в приведенном выше уравнении. 72 легко делится на несколько небольших чисел: 1, 2, 3, 4, 6, 8, 9 и 12. Это хорошее приближение для годового начисления сложных процентов по типичным ставкам (от 6% до 10%). Приближения менее точны при более высоких процентных ставках.