Среднее геометрическое - это еще один способ найти среднее значение набора чисел, но вместо того, чтобы складывать значения и делить, как при нахождении среднего арифметического, вы умножаете их вместе, прежде чем извлекать корень. Среднее геометрическое можно использовать для расчета средней доходности в финансах или для отображения того, насколько что-то выросло за определенный период времени. Чтобы найти среднее геометрическое, умножьте все значения вместе перед извлечением корня n-й степени, где n равно общему количеству значений в наборе. Вы также можете использовать логарифмические функции на вашем калькуляторе для вычисления среднего геометрического, если хотите.
Шаги
Справка по среднему геометрическому

Шпаргалка по геометрическому среднему с двумя числами

Шпаргалка по геометрическому среднему с тремя и более числами
Метод 1 из 2: определение среднего геометрического набора значений
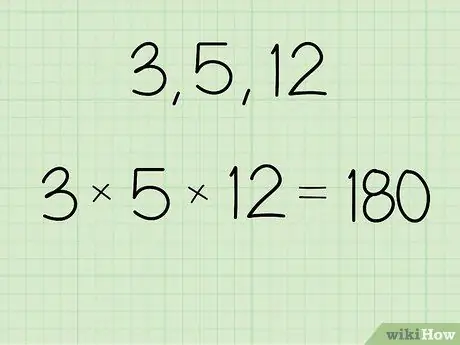
Шаг 1. Умножьте значения, для которых вы хотите найти среднее геометрическое
Вы можете использовать калькулятор или посчитать вручную, когда найдете продукт. Умножьте все числа в вычисляемом наборе, чтобы найти продукт. Запишите продукт, чтобы не забыть его.
- Например, если установлено значение 3, 5 и 12, вы должны написать: (3 x 5 x 12) = 180.
- В качестве другого примера, если вы хотите найти среднее геометрическое для наборов 2 и 18, напишите: (2 x 18) = 36.

Шаг 2. Найдите корень n-й степени от произведения, где n - количество значений
Подсчитайте, сколько значений содержится в наборе, в котором вы вычисляете среднее геометрическое для значения n. Используйте значение n, чтобы определить, какой корень вам нужен для продукта. Например, возьмите квадратный корень, если у вас 2 значения, кубический корень, если у вас 3 значения, и так далее. С помощью калькулятора решите уравнение и запишите ответ.
- Например, для набора из 3, 5 и 12 напишите: ∛ (180) ≈ 5,65.
- Во втором примере с набором 2 и 18 напишите: √ (36) = 6.
Вариант:
Вы также можете записать значение в виде экспоненты 1 / n, если это проще ввести в калькулятор. Например, для набора 3, 5 и 12 вы можете написать (180)1/3 вместо ∛ (180).
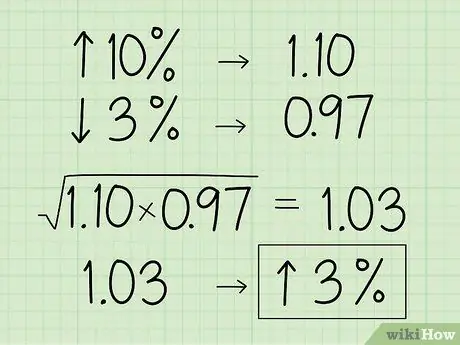
Шаг 3. Преобразуйте проценты в их десятичные эквиваленты множителя
Если набор чисел записан как увеличение или уменьшение в процентах, избегайте использования значения процента в среднем геометрическом, поскольку это исказит ваши результаты. Если процент увеличивается, переместите десятичную запятую на 2 пробела влево и прибавьте к ней 1. Если есть процентное уменьшение, переместите десятичную запятую на 2 разряда влево и вычтите ее из 1.
- Например, вы хотите найти среднее геометрическое значение объекта, которое увеличивается на 10%, а затем падает на 3%.
- Преобразуйте 10% в десятичную дробь и прибавьте к ней 1, чтобы получить 1,10.
- Затем преобразуйте 3% в десятичную дробь и вычтите из 1, чтобы получить 0,97.
- Используйте 2 десятичных значения, чтобы найти среднее геометрическое: √ (1,10 x 0,97) ≈ 1,03.
- Преобразуйте число обратно в проценты, переместив десятичную запятую на 2 разряда вправо и вычтя из нее 1, чтобы получить общее увеличение значения на 3%.
Метод 2 из 2: Расчет среднего геометрического с помощью логарифмов

Шаг 1. Добавьте логарифмические значения для каждого числа в наборе
Функция LOG берет значение из десятичной системы и определяет, сколько раз вам нужно умножить 10, чтобы получить это значение. Найдите функцию LOG на калькуляторе, который обычно находится слева от клавиатуры. Нажмите кнопку LOG и введите первое значение в наборе. Введите «+», прежде чем вводить ЖУРНАЛ для второго значения. Продолжайте разделять функции LOG для каждого значения знаком плюс, прежде чем найти сумму.
- Например, с набором из 7, 9 и 12 вы должны ввести log (7) + log (9) + log (12), прежде чем нажать «=» на вашем калькуляторе. Когда вы решите функции, ваша сумма будет около 2,878521796.
- Вы также можете вычислить каждый логарифм отдельно, прежде чем складывать ответы вместе.
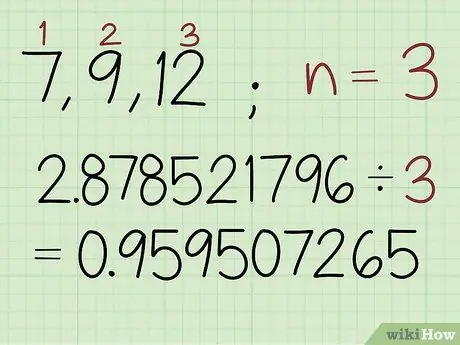
Шаг 2. Разделите сумму логарифмических значений на количество значений в наборе
Подсчитайте количество значений в вашем наборе, а затем разделите только что найденную сумму на это число. Ответ, который вы получите, будет логарифмическим значением среднего геометрического.
В этом примере набор из 3 чисел, поэтому введите: 2,878521796 / 3 ≈ 0,959507265

Шаг 3. Возьмите антилогарифм частного, чтобы определить среднее геометрическое
Функция antilog - это функция, обратная функции LOG на вашем калькуляторе, и она преобразует значение обратно в основание 10. Найдите символ «10Икс»На вашем калькуляторе, что обычно является второстепенной функцией кнопки LOG. Нажмите кнопку «2nd» в верхнем левом углу калькулятора, а затем кнопку LOG, чтобы активировать антилог. Введите частное, которое вы нашли на последнем шаге, прежде чем решать уравнение.
В этом примере ваш калькулятор будет читать: 10(0.959507265) ≈ 9.11.
подсказки
- Вы не можете найти среднее геометрическое отрицательных чисел.
- Любой набор, в котором есть 0, будет иметь среднее геометрическое 0.
