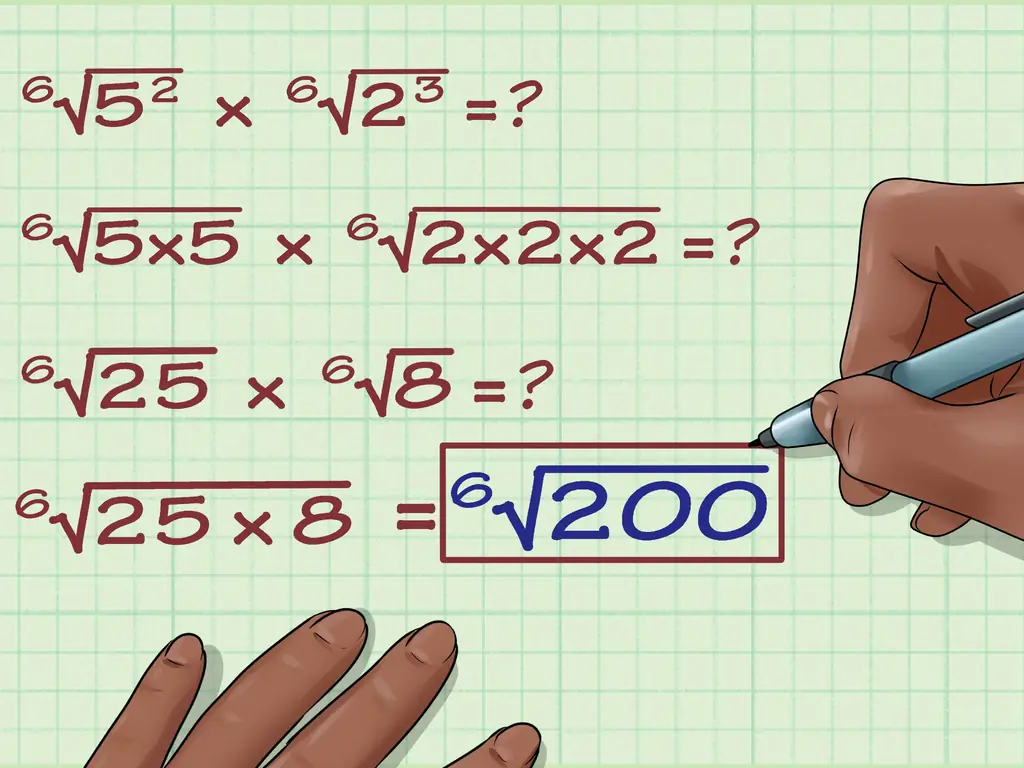Символ корня (√) представляет собой квадратный корень из числа. Вы можете встретить радикальный символ в алгебре или даже в столярном деле или другом ремесле, которое связано с геометрией или вычислением относительных размеров или расстояний. Вы можете перемножить любые два корня с одинаковыми индексами (степенями корня). Если радикалы не имеют одинаковых индексов, вы можете манипулировать уравнением, пока они не появятся. Если вы хотите знать, как умножить радикалы с коэффициентами или без них, просто выполните следующие действия.
Шаги
Метод 1 из 3: умножение радикалов без коэффициентов
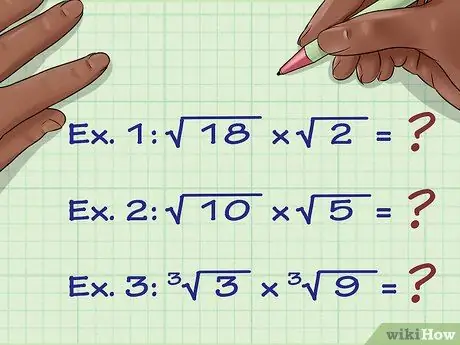
Шаг 1. Убедитесь, что радикалы имеют одинаковый индекс
Для умножения радикалов основным методом они должны иметь одинаковый индекс. «Индекс» - это очень маленькое число, написанное слева от самой верхней строки в радикальном символе. Если порядкового номера нет, то считается, что радикал является квадратным корнем (индекс 2) и может быть умножен на другие квадратные корни. Вы можете умножать радикалы с разными индексами, но это более сложный метод, который будет объяснен позже. Вот два примера умножения с использованием радикалов с одинаковыми индексами:
- Бывший. 1: √ (18) x √ (2) =?
- Бывший. 2: √ (10) x √ (5) =?
- Бывший. 3: 3√ (3) х 3√(9) =?

Шаг 2. Умножьте числа под коренными знаками
Затем просто умножьте числа под знаком корня или квадратного корня и оставьте их там. Вот как это сделать:
- Бывший. 1: √ (18) x √ (2) = √ (36)
- Бывший. 2: √ (10) x √ (5) = √ (50)
- Бывший. 3: 3√ (3) х 3√(9) = 3√(27)

Шаг 3. Упростите радикальные выражения
Если вы перемножили радикалы, есть большая вероятность, что их можно упростить до идеальных квадратов или идеальных кубов или что их можно упростить, найдя идеальный квадрат в качестве множителя конечного произведения. Вот как это сделать:
- Бывший. 1: √ (36) = 6. 36 - это полный квадрат, потому что это произведение 6 x 6. Квадратный корень из 36 равен 6.
-
Бывший. 2: √ (50) = √ (25 x 2) = √ ([5 x 5] x 2) = 5√ (2). Хотя 50 не является точным квадратом, 25 - это коэффициент 50 (потому что оно делится на число поровну) и является полным квадратом. Вы можете разбить 25 на множители 5 x 5 и вынести единицу 5 из знака квадратного корня, чтобы упростить выражение.
Вы можете думать об этом так: если вы отбросите 5 обратно под радикал, оно умножится само на себя и снова станет 25
- Бывший. 3:3√ (27) = 3. 27 - идеальный куб, потому что это произведение 3 x 3 x 3. Следовательно, кубический корень из 27 равен 3.
Метод 2 из 3: умножение радикалов на коэффициенты

Шаг 1. Умножьте коэффициенты
Коэффициенты - это числа вне корня. Если коэффициент не задан, то можно понимать, что коэффициент равен 1. Умножьте коэффициенты вместе. Вот как это сделать:
-
Бывший. 1: 3√ (2) x √ (10) = 3√ (?)
3 х 1 = 3
-
Бывший. 2: 4√ (3) x 3√ (6) = 12√ (?)
4 х 3 = 12
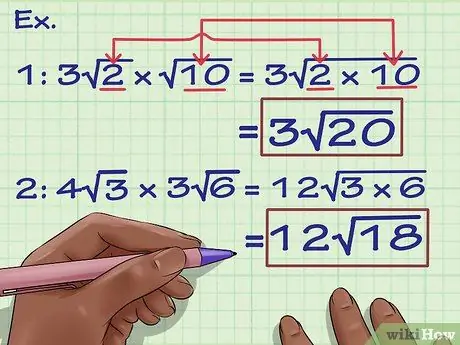
Шаг 2. Умножьте числа внутри радикалов
После того, как вы умножили коэффициенты, вы можете умножить числа внутри радикалов. Вот как это сделать:
- Бывший. 1: 3√ (2) x √ (10) = 3√ (2 x 10) = 3√ (20)
- Бывший. 2: 4√ (3) x 3√ (6) = 12√ (3 x 6) = 12√ (18)

Шаг 3. Упростите продукт
Затем упростите числа под радикалами, ища полные квадраты или кратные числам под радикалами, которые являются полными квадратами. После того, как вы упростили эти термины, просто умножьте их на соответствующие коэффициенты. Вот как это сделать:
- 3√ (20) = 3√ (4 x 5) = 3√ ([2 x 2] x 5) = (3 x 2) √ (5) = 6√ (5)
- 12√ (18) = 12√ (9 x 2) = 12√ (3 x 3 x 2) = (12 x 3) √ (2) = 36√ (2)
Метод 3 из 3: умножение радикалов с разными индексами
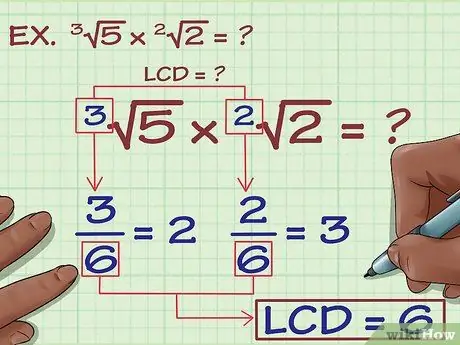
Шаг 1. Найдите НОК (наименьшее общее кратное) индексов
Чтобы найти НОК индексов, найдите наименьшее число, которое без остатка делится на оба индекса. Найдите НОК индексов следующего уравнения:3√ (5) х 2√(2) =?
Индексы - 3 и 2. 6 - это НОК этих двух чисел, потому что это наименьшее число, которое делится без остатка как на 3, так и на 2. 6/3 = 2 и 6/2 = 3. Чтобы умножить радикалы, оба числа индексы должны быть 6
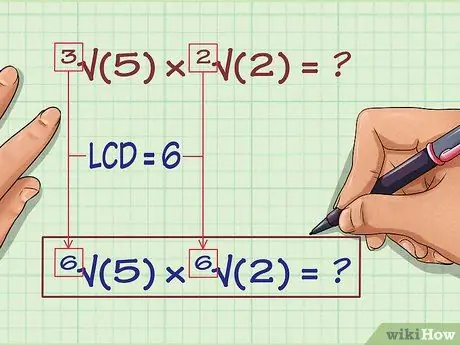
Шаг 2. Запишите каждое выражение с новым LCM в качестве индекса
Вот как будут выглядеть выражения в уравнении с их новыми индексами:
6√ (5) х 6√(2) =?
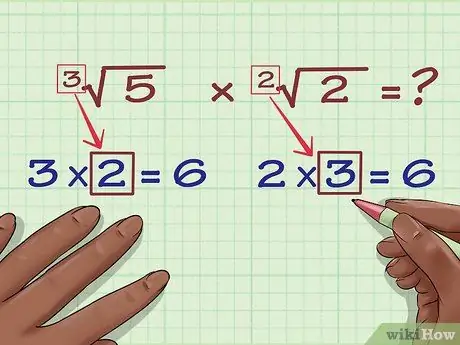
Шаг 3. Найдите число, на которое вам нужно умножить каждый исходный индекс, чтобы найти НОК
Для выражения 3√ (5), вам нужно умножить индекс 3 на 2, чтобы получить 6. Для выражения 2√ (2), вам нужно будет умножить индекс 2 на 3, чтобы получить 6.

Шаг 4. Сделайте это число экспонентой числа внутри корня
Для первого уравнения сделайте число 2 показателем степени над числом 5. Для второго уравнения сделайте число 3 показателем степени над числом 2. Вот как это будет выглядеть:
- 2 6√(5) = 6√(5)2
- 3 6√(2) = 6√(2)3
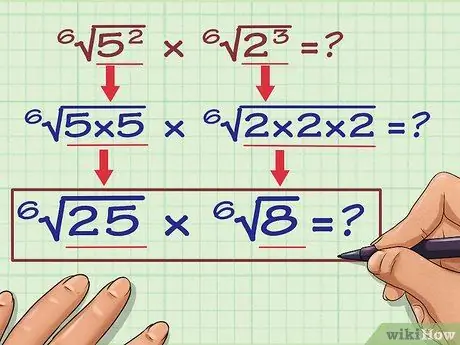
Шаг 5. Умножьте числа внутри радикалов на их показатель степени
Вот как это сделать:
- 6√(5)2 = 6√ (5 х 5) = 6√25
- 6√(2)3 = 6√ (2 х 2 х 2) = 6√8
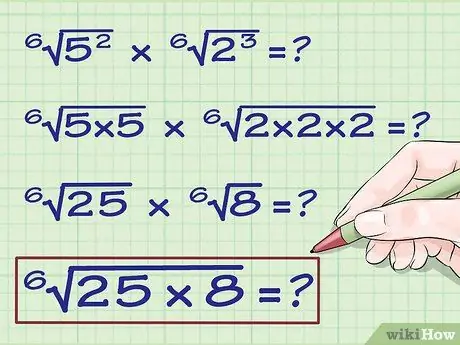
Шаг 6. Поместите эти числа под один корень
Поместите их под корень и соедините знаком умножения. Вот как бы выглядел результат: 6√ (8 х 25)

Шаг 7. Умножьте их
6√ (8 х 25) = 6√ (200). Это окончательный ответ. В некоторых случаях вы можете упростить эти выражения - например, вы можете упростить это выражение, если найдете число, которое можно умножить само на себя в шесть раз, что является множителем 200. Но в этом случае выражение не может можно еще больше упростить.
Видео - с помощью этой службы некоторая информация может быть передана YouTube
подсказки
- Если «коэффициент» отделен от радикального знака знаком «плюс» или «минус», это вовсе не коэффициент - это отдельный термин, с которым нужно работать отдельно от радикала. Если радикал и другой член заключены в один и тот же набор круглых скобок - например, (2 + (квадратный корень) 5), вы должны обрабатывать как 2, так и (квадратный корень) 5 отдельно при выполнении операций внутри круглых скобок, но при выполнении операций вне скобок вы должны обрабатывать (2 + (квадратный корень) 5) как единое целое.
- Радикальные знаки - это еще один способ выражения дробных показателей. Другими словами, квадратный корень любого числа совпадает с этим числом в степени 1/2, кубический корень любого числа совпадает с этим числом в степени 1/3 и так далее.
- «Коэффициент» - это число, если оно есть, помещенное непосредственно перед знаком корня. Так, например, в выражении 2 (квадратный корень) 5, 5 находится под знаком корня, а цифра 2 вне корня - это коэффициент. Когда радикал и коэффициент помещаются вместе, это означает то же самое, что и умножение радикала на коэффициент, или, продолжая пример, 2 * (квадратный корень) 5.